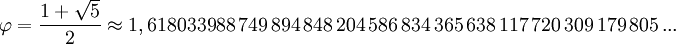
Se trata de un número que posee muchas propiedades interesantes y que fue descubierto en la antigüedad, no como “unidad” sino como relación o proporción. Esta proporción se encuentra tanto en algunas figuras geométricas como en las partes de un cuerpo, y en la naturaleza como relación entre cuerpos, en la morfología de diversos elementos tales como caracolas, nervaduras de las hojas de algunos árboles, el grosor de las ramas, proporciones humanas, etc.
Historia del número áureo
Existen numerosos textos que sugieren que el número áureo se encuentra como proporción en ciertas estelas Babilonias y Asirias de alrededor de 2000 a. C.. Sin embargo no existe documentación histórica que indique que el número áureo fue usado conscientemente por los arquitectos o artistas en la construcción de las estelas. También es importante notar que cuando se mide una estructura complicada es fácil obtener resultados curiosos si se tienen muchas medidas disponibles. Además para que se pueda considerar que el número áureo está presente, las medidas deben tomarse desde puntos relativamente obvios del objeto y este no es el caso de los elaborados teoremas que defienden la precencia del número áureo. Por todas estas razones Mario Livio concluye que es muy improbable que los Babilonios hayan descubierto el Número Áureo.
En la antigua Grecia se utilizó para establecer las proporciones de los templos, tanto en su planta como en sus fachadas. Por aquel entonces no recibía ningún nombre especial, ya que era algo tan familiar entre los antiguos griegos que "la división de un segmento en media extrema y razón" era conocido generalmente como "la sección". En el Partenón, Fidias también lo aplicó en la composición de las esculturas. (la denominación Fi, por ser la primera letra de su nombre, la efectuó en 1900 el matemático Mark Barr en su honor).
Platón (c. 428-347 a. C.), consideró la sección áurea como la mejor de todas las relaciones matemáticas y la llave a la física del cosmos.
La sección áurea se usó mucho en el Renacimiento, particularmente en las artes plásticas y la arquitectura. Se consideraba la proporción perfecta entre los lados de un rectángulo.
Da Vinci hizo las ilustraciones para una disertación publicada por Luca Pacioli en 1509 titulada De Divina Proportione, quizás la referencia más temprana en la literatura a otro de sus nombres, el de "Divina Proporción". Este libro contiene los dibujos hechos por Leonardo da Vinci de los cinco sólidos platónicos. Es probable que fuera Leonardo quien diera por primera vez el nombre de sectio áurea. En 1525, Alberto Durero publica Instrucción sobre la medida con regla y compás de figuras planas y sólidas donde describe cómo trazar con regla y compás la espiral basada en la sección áurea, que se conoce como “espiral de Durero”.
Los artistas de Renacimiento utilizaron la sección áurea en múltiples ocasiones tanto en pintura, escultura como arquitectura para lograr el equilibrio y la belleza. Leonardo da Vinci, por ejemplo, la utilizó para definir todas las proporciones fundamentales en su pintura La última cena, desde las dimensiones de la mesa, hasta la disposición de Cristo y los discípulos sentados, así como las proporciones de las paredes y ventanas al fondo.
Leonardo da Vinci, en su cuadro de la Gioconda (o Mona Lisa) utilizó rectángulos áureos para plasmar el rostro de Mona Lisa. Se pueden localizar muchos detalles de su rostro, empezando porque el mismo rostro se encuadra en un rectángulo áureo.
El astrónomo Johannes Kepler (1571-1630), descubridor de la naturaleza elíptica de las órbitas de los planetas alrededor del Sol, mencionó también la divina proporción: “La geometría tiene dos grandes tesoros: uno es el teorema de Pitágoras; el otro, la división de una línea entre el extremo y su proporcional. El primero lo podemos comparar a una medida de oro; el segundo lo debemos denominar una joya preciosa”. Y, creyente como era dijo: “no cabe duda de que Dios es un gran matemático”.
Hoy en día la sección áurea se puede ver en multitud de diseños. El más conocido y difundido sería la medida de las tarjetas de crédito, la cual también sigue dicho patrón, así como nuestro carné de identidad y también en las cajetillas de cigarrillos.
En la arquitectura moderna sigue usándose; por ejemplo, está presente en el conocido edificio de la ONU en Nueva York, el cual no es más que un gran prisma rectangular cuya cara mayor sigue las citadas proporciones.
El rostro de la Gioconda proporcionado con rectángulos áureos.
La sección áurea en la naturaleza
En la naturaleza, hay muchos elementos relacionados con la sección áurea:
* Según el propio Leonardo de Pisa Fibonacci, en su Libro de los ábacos, la secuencia puede ayudar a calcular casi perfectamente el número de pares de conejos n meses después de que una primera pareja comienza a reproducirse (suponiendo que los conejos se empiezan a reproducir cuando tienen dos meses de edad).
* La relación entre la cantidad de abejas macho y abejas hembra en un panal.
* La relación entre la distancia entre las espiras del interior espiralado de cualquier caracol (no sólo del nautilus)
Hay por lo menos tres espirales logarítmicas en las que se puede encontrar de alguna manera al número áureo. La primera de ellas se caracteriza por la relación constante igual al número áureo entre los radiovectores de puntos situados en dos evolutas consecutivas en una misma dirección y sentido. Las conchas del Fusus antiquus, del Murex, de Scalaria pretiosa, de Facelaria y de Solarium trochleare, entre otras, siguen este tipo de espiral de crecimiento.
Se debe entender que en toda consideración natural, aunque involucre a las ciencias consideradas más matemáticamente desarrolladas, como la Física, ninguna relación o constante que tenga un número infinito de decimales puede llegar hasta el límite matemático, porque en esa escala no existiría ningún objeto físico. La partícula elemental más diminuta que se pueda imaginar es infinitamente más grande que un punto en una recta. Las leyes observadas y descriptas matemáticamente en los organismos las cumplen transgrediéndolas orgánicamente. (Esto último es una paráfrasis de un pensamiento de Ruskin citado en la página 139 de la referencia 2).
* La relación entre los lados de un pentáculo *.
* La relación entre los lados de un pentágono *.
* La disposición de los pétalos de las flores (el papel del número áureo en la botánica recibe el nombre de Ley de Ludwig).
* La distribución de las hojas en un tallo
Ver: Sucesión de Fibonacci, La sucesión de Fibonacci, el número áureo y la sección áurea en la naturaleza (punto 7 del artículo)
* La relación entre las nervaduras de las hojas de los árboles
* La relación entre el grosor de las ramas principales y el tronco, o entre las ramas principales y las secundarias (el grosor de una equivale a Φ tomando como unidad la rama superior).
* La distancia entre las espirales de una piña.
* La Anatomía de los humanos se basa en una relación Φ exacta, así vemos que:
* La relación entre la altura de un ser humano y la altura de su ombligo.
* La relación entre la distancia del hombro a los dedos y la distancia del codo a los dedos.
* La relación entre la altura de la cadera y la altura de la rodilla.
* La relación entre el primer hueso de los dedos (metacarpiano) y la primera falange, o entre la primera y la segunda, o entre la segunda y la tercera, si dividimos todo es phi.
* La relación entre el diámetro de la boca y el de la nariz
* Es phi la relación entre el diámetro externo de los ojos y la línea inter-pupilar
* Cuando la tráquea se divide en sus bronquios, si se mide el diámetro de los bronquios por el de la tráquea se obtiene phi, o el de la aorta con sus dos ramas terminales (ilíacas primitivas).
* Está comprobado que la mayor cantidad de números phi en el cuerpo y el rostro hacen que la mayoría de las personas reconozcan a esos individuos como guapos, bellos y proporcionados. Si se miden los números phi de una población determinada y se la compara con una población de modelos publicitarios, estos últimos resultan acercarse más al número phi.
Concha de nautilus en espiral logarítmica
La sección áurea en el arte
* Relaciones arquitectónicas en las Pirámides de Egipto.
En cuanto a la Gran Pirámide de Gizeh la afirmación de Herodoto de que el cuadrado de la altura es igual a la superficie de una cara es posible únicamente si la semi-sección meridiana de la pirámide es proporcional al triángulo rectángulo ,
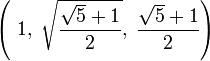donde 1 representa proporcionalmente a la mitad de la base, la raíz cuadrada del número áureo a la altura hasta el vértice inexistente y el número áureo o hipotenusa del triángulo a la apotema de la Gran Pirámide. Esta tesis ha sido defendida por los matemáticos Jarolimek, K. Kleppisch y W. A. Price (ver referencias), cuenta con el testimonio histórico de Herodoto y resulta teóricamente con sentido, aunque una construcción de semejante tamaño deba contener errores inevitables a toda obra arquitectónica y a la misma naturaleza de la tecnología humana, que en la práctica puede manejar únicamente números racionales. Los demás investigadores famosos se inclinan por la hipótesis de que los constructores intentaron una cuadratura del círculo, pues la raíz cuadrada del número áureo se aproxima mucho al cociente de 4 sobre π. Pero una construcción tal, aunque se conociera π con una aproximación grande, carecería completamente de sentido matemático. No obstante, en base a mediciones no es posible elegir entre una u otra pues la diferencia sobre el monumento real no es mayor a 14,2 cm y esta pequeña variación queda enmascarada por las incertidumbres de las medidas, los errores constructivos y, principalmente, porque la pirámide perdió el revestimiento en manos de los primeros constructores de El Cairo. Para que esto quede más claro, una precisión del 1 por mil en una base de 230 metros equivale a 23 centímetros y en la altura está en el orden de la diferencia real que debería existir entre ambas posibilidades.
* La relación entre las partes, el techo y las columnas del Partenón, en Atenas (s. V a. C.).
Durante el primer cuarto del siglo XX, Jay Hambidge, de la Universidad de Yale, se inspiró en un pasaje del Theeteto de Platón para estudiar las proporciones relativas de las superficies, algo muy natural cuando se trata de obras arquitectónicas.
Dos rectángulos no semejantes se distinguen entre sí por el cociente de su lado mayor por el menor, número que basta para caracterizar a estas figuras y que denominó módulo del rectángulo. Un cuadrado tiene módulo 1 y el doble cuadrado módulo 2. Aquellos rectángulos cuyos módulos son números enteros o racionales fueron denominados "estáticos" y los que poseen módulos irracionales euclidianos, o sea, expresables algebraicamente como raíces de ecuaciones cuadráticas o reducibles a ellas, "dinámicos". El doble cuadrado es a la vez estático y dinámico, pues 2 es la raíz cuadrada de 4. Un ejemplo de rectángulo dinámico elemental es aquel que tiene por lado mayor a la raíz cuadrada de 5 y por lado menor a la unidad, siendo su módulo la raíz cuadrada de 5.
Posteriormente Hambidge estudió a los monumentos y templos griegos y llegó a encuadrar el frontón del Partenón en un rectángulo de módulo \frac {4\Phi - 2}{\Phi + 1}. Por medio de cuatro diagonales suministra las principales proporciones verticales y horizontales. Este rectángulo es descompuesto en seis de módulo \sqrt {5} y cuatro cuadrados.
Como dato adicional para indicar la complejidad del tratamiento del edificio se tiene que en 1837 fueron descubiertas correcciones ópticas en el Partenón. El templo tiene tres vistas principales y si sus columnas estuvieran efectivamente a plomo, todas sus líneas fuesen paralelas y perfectamente rectas y los ángulos rectos fueran exactos, por las propiedades de la visión humana el conjunto se vería más ancho arriba que en la base, sus columnas se percibirían inclinadas hacia afuera y la línea que fundamenta el techo sobre las columnas se vería como una especie de catenaria, con los extremos del edificio aparentemente más altos que el centro. Los constructores hicieron la construcción compensando estos efectos de ilusión óptica inclinando o curvando en sentido inverso a los elementos involucrados. Así las columnas exteriores,en ambos lados del frente, están inclinadas hacia adentro en un ángulo de 2,65 segundos de arco, mientras que las que están en el medio tienen una inclinación de 2,61 segundos de arco. La línea que formarían los dinteles entre columnas y que constituye la base del triángulo que corona el edificio, en realidad es un ángulo de 2,64 segundos de arco con el vértice más elevado que los extremos. De esta forma, y con otras correcciones que no se mencionan aquí, se logra que cualquier observador que se sitúe en los tres puntos principales de vista vea todo el conjunto paralelo, uniforme y recto.
* En los violines, la ubicación de las efes (los “oídos”, u orificios en la tapa) se relaciona con el número áureo.
* El número áureo aparece en las relaciones entre altura y ancho de los objetos y personas que aparecen en las obras de Miguel Ángel, Durero y Da Vinci, entre otros.
* Las relaciones entre articulaciones en el hombre de Vitruvio y en otras obras de Leonardo da Vinci.
* En las estructuras formales de las sonatas de Mozart, en la Quinta Sinfonía de Beethoven, en obras de Schubert y Debussý (estos compositores probablemente compusieron estas relaciones de manera inconsciente, basándose en equilibrios de masas sonoras).
* En la pág. 61 de la novela de Dan Brown El código Da Vinci aparece una versión desordenada de los primeros ocho números de Fibonacci (13, 3, 2, 21, 1, 1, 8, 5), que funcionan como una pista dejada por el curador del museo del Louvre, Jacques Saunière. En las pp. 121 a 123 explica algunas de las apariciones de este número fi (1,618) en la naturaleza.
* En el episodio “Sabotaje” de la serie de televisión NUMB3RS (primera temporada, 2005), el genio de la matemática Charlie Eppes menciona que el número fi se encuentra en la estructura de los cristales, en la espiral de las galaxias y en la concha del nautilus.
* Arte Póvera, movimiento artístico italiano de los años 1960, muchas de cuyas obras se basan en esta sucesión.
* En la cinta de Darren Aronofsky Pi, el orden del caos el personaje central, Max Cohen, explica la relación que hay entre los números de Fibonacci y la sección áurea, aunque denominándola incorrectamente como Theta (θ) en vez de Phi (Φ).
Hombre de virtuvio
El número áureo en la música
Autores como Bártok, Messiaen y Stockhausen, entre otros, compusieron obras cuyas unidades formales se relacionan (a propósito) con la sección áurea.
El compositor mexicano Silvestre Revueltas (1899-1945) utilizó también el número áureo en su obra Alcancías, para organizar las partes (unidades formales).
El grupo de rock progresivo norteamericano Tool, en su disco Lateralus (2001) hacen múltiples referencias al número áureo y a la secuencia Fibonacci, sobre todo en la canción que da nombre al disco, pues los versos de la misma están cantados de forma que el número de sílabas pronunciadas en cada uno van componiendo dicha secuencia. Además la voz entra en el minuto 1:37, que pasado al sistema decimal coincide muy aproximadamente con el número áureo.
La sección áurea en el pentáculo
Existe la relación del número áureo también en el pentáculo o pentalfa, un símbolo pagano, más tarde acogido por la iglesia católica para representar a la Virgen María, y también por Leonardo da Vinci para asentar en él al hombre de Vitruvio.
Gráficamente el número áureo es la relación entre el lado del pentágono regular y la recta que une dos vértices no consecutivos de éste. Si se toma como unidad un lado del pentágono interior, cualquier línea que marca los brazos de la estrella mide Φ. También la longitud total de cualquiera de las cinco líneas que atraviesan la estrella mide Φ3, mientras que la suma del lado interior y cualquiera de sus brazos es Φ2.
Teniendo en cuenta la gran simetría de este símbolo se observa que dentro del pentágono interior es posible dibujar una nueva estrella, con una recursividad hasta el infinito. Del mismo modo, es posible dibujar un pentágono por el exterior, que sería a su vez el pentágono interior de una estrella más grande.
Al medir la longitud total de una de las cinco líneas del pentáculo interior, resulta igual a la longitud de cualquiera de los brazos de la estrella mayor, o sea Φ.
Pentaculo.
